해시테이블 : 키 / 값 대응으로 이루어진 표와 같은 자료구조
- 키 : 해시 테이블에 대한 입력
- 값 : 키에 대응되는 데이터
예시
- 전화번호부 : 이름 = 키, 전화번호 = 값
- 책 : ISBN = 키, 책 제목 = 값
운영체제 내부에서의 사용
- 리눅스 커널 (아래 이미지 참고)

- 페이지 캐시, 아이노드 캐시 등으로 활용하기도 함
해시 테이블 구조와 동작
- 키를 통해 얻고자 하는 데이터는 bucket에 저장,
(버킷은 여러개 존재하며 버킷들은 배열을 형성)
- 해시 함수는 키를 인자로 버킷에 접근할 인덱스 반환
(키를 해시 함수에 통과시켜 원하는 버킷에 접근)
[해시 함수]

해시 함수 : 임의의 길이의 입력 데이터를 고정된 길이의 해시값으로 변환하는 단방향 함수.
- 동일한 입력에 대해 항상 동일한 출력을 제공
- 역으로 원래 데이터를 복원하기 어려운 특성을 가진다

해시 알고리즘
- 해시 함수의 연산 방법
- 대표적인 해시 알고리즘 : MD5, SHA-1, SHA-256, SHA-512, SHA3, HMAC 등
- 같은 데이터라도, 적용된 해시 알고리즘이 다르면 해시 값의 길이나 값이 달라진다
-> 위의 특성들로 인해, 해시 함수는 무작위 값을 만들거나 단방향 암호를 만들 때, 데이터 무결성을 검증하기 위해 사용한다
비밀번호 저장에서의 해시 값 사용
* 웹 서비스 로그인 시 아이디, 비밀번호를 입력하더라도 서비스 관리자가 비밀번호를 알 수 있는 것은 아님 *
- 비밀번호를 비롯한 개인 정보 저장시 단방향 암호로 저장되도록 규제. (개인정보 안정성 확보 조치 기준 제7조 - 개인 정보의 암호화)
해시 테이블의 장/단점
- 장점 : 빠른 검색 속도.
일반적인 상황에서 해시 테이블을 사용한 검색, 삽입, 삭제 연산의 시간 복잡도는 O(1)이다.
-> 입력과 무관하게 항상 일정한 속도 보장
- 단점
1. 많은 메모리 공간 소모
- 데이터가 매우 많을 경우, 공간 복잡도는 우수하지 않음을 의미
2. 해시 충돌 문제
[해시 충돌]
서로 다른 키에 같은 해시 값이 대응되는 상황.

*해시 충돌로 인해 발생할 수 있는 문제
- 대표적 해시 함수중 하나인 SHA-1 해시 충돌 사례
shatterd-1.pdf와 shatterd-2.pdf는 다른 파일이지, 두 파일 데이터에 대한 해시값을 구하면 SHA-1 알고리즘상 동일한 해시 값 도출
* 해시 충돌 해결법
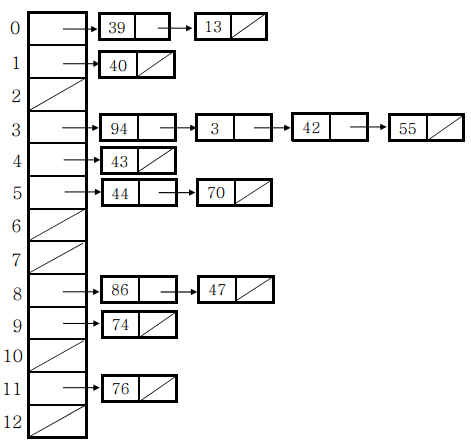
1. chaining : 충돌이 발생한 데이터를 연결 리스트로 추가
- 서로 다른 키가 같은 위치로 해시되어도, 연결 리스트 노드만 추가
- 충돌이 발생할 때마다 연결 리스트의 노드가 추가된다면 성능 저하 우려가 있음. (n개의 데이터가 모두 충돌한다면 탐색 성능이 O(N)으로 저하)
2. 개방 주소법, open addressing : 충돌 발생시, 충돌이 발생한 버킷의 인덱스가 아닌 다른 인덱스에 데이터를 저장.
- 조사, probe : 충돌이 발생했을 때 비어있는 다른 버킷의 인덱스를 찾는 과정.
* 선형 탐사법, linear probing
- 충돌 발생한 인덱스의 다음 인덱스부터 순차적으로 사용 가능한 인덱스 탐색.
- 해시 함수를 f, 키를 key 라고 할 때
해시값인 f(key)에서 충돌 발생시 f(key) + 1, f(key) + 2, f(key) + 3, ... 순으로 사용 가능한 인덱스 탐색

-> 선형 조사법의 문제 - 데이터 군집화(clustering)
- 해시 충돌이 발생하는 인덱스 인근에 충돌 발생한 여러 데이터가 물려 저장될 수 있음(군집화)
- 군집화 발생 시, 오랜 순차 탐색이 필요 (성능 악화)
* 제곱 탐사법, quadratic probing) : 순차적 탐색은 동일하나, 고정폭이 아닌 제곱으로 늘어나는 탐사법.
- 선형 탐사법보다 데이터 군집화 문제 완화는 가능하지만, 해결하는 근본적인 방법이라고 보기는 어렵다.
* 이중 해싱, double hashing
- 2개의 해시 함수를 사용.
- 충돌 발생 시 보조 해시 함수 해시 값만큼 떨어진 거리에 위치한 인덱스 탐색
- 충돌 발생 시, f(key) + g(key)에서 인덱스 탐색
- 위에서도 충돌 발생 시 f(key) +2g(key) 에서 인색스 탐색 ...
-> 해시 함수를 통해 무작위로 인덱스가 생성될 수 있다면 군집화 문제를 상당 부분 피할 수 있음

자바스크립트 Map
const phoneBook = new Map();
phoneBook.set("홍길동", "010-1234-5678");
console.log(phoneBook.get("홍길동")); // 출력: 010-1234-5678
자바스크립트의 Map과 Set
- 자바스크립트에서 Map과 Set은 해시테이블을 기반으로 구현되어 있으며, 키-값 쌍의 저장과 고유한 값의 저장에 유용
- Map은 키의 순서를 유지하며, 다양한 타입의 키를 사용할 수 있다.
- Set은 중복을 허용하지 않는 고유한 값의 집합을 저장할 때 사용된다.
참고 자료
- https://youtu.be/dUs_hSG5YNE?si=uqaZ8vk9xpECBz-O
- https://developer.mozilla.org/ko/docs/Web/JavaScript/Reference/Global_Objects/Map
- https://developer.mozilla.org/ko/docs/Web/JavaScript/Reference/Global_Objects/Set
'CS' 카테고리의 다른 글
| 자료구조 - 스택과 큐 (0) | 2025.05.24 |
|---|---|
| 자료구조 - 배열과 연결 리스트/ js 연결리스트 구현 (0) | 2025.05.20 |
| 자료구조의 큰 그림 / 시간복잡도, 공간 복잡도 (0) | 2025.05.19 |
| 운영체제 - 파일시스템 (0) | 2025.05.17 |
| 운영체제의 메모리 관리 기법 - 가상메모리 (0) | 2025.05.15 |